Abstract

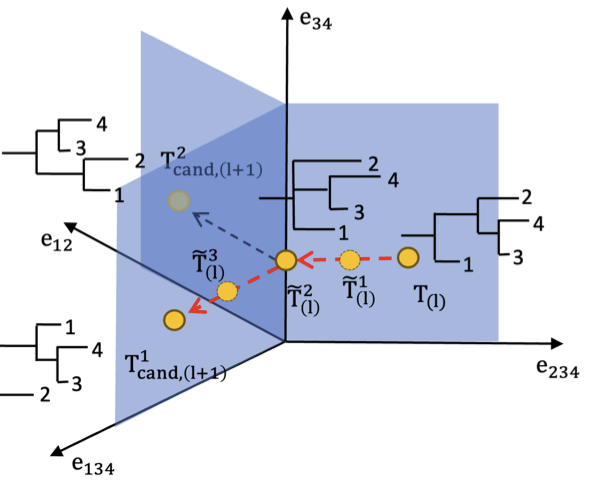
Ultrametric matrices arise as covariance matrices in latent tree models for multivariate data with hierarchically correlated components. As a parameter space in a model, the set of ultrametric matrices is neither convex nor a smooth manifold, and focus in literature has hitherto mainly been restricted to estimation through projections and relaxation-based techniques. Leveraging the link between an ultrametric matrix and a rooted tree, we equip the set of ultrametric matrices with a convenient geometry based on the well-known geometry of phylogenetic trees, whose attractive properties (e.g. unique geodesics and Fr´echet means) the set of ultrametric matrices inherits. This results in a novel representation of an ultrametric matrix by coordinates of the tree space, which we then use to define a class of Markovian and consistent prior distributions on the set of ultrametric matrices in a Bayesian model, and develop an efficient algorithm to sample from the posterior distribution that generates updates by making intrinsic local moves along geodesics within the set of ultrametric matrices. In simulation studies, our proposed algorithm restores the underlying matrices with posterior samples that recover the tree topology with a high frequency of true topology and generate element-wise credible intervals with a high nominal coverage rate. We use the proposed algorithm on the pre-clinical cancer data to investigate the mechanism similarity by constructing the underlying treatment tree and identify treatments with high mechanism similarity also target correlated pathways in biological literature.