Abstract

This paper presents a model-based method for clustering multivariate binary observations that incorporates constraints consistent with the scientific context. The approach is motivated by the precision medicine problem of identifying autoimmune disease patient subsets or classes who may require different treatments. We start with a family of restricted latent class models or RLCMs (e.g., Xu and Shang, 2018). However, in the motivating example and many others like it, the unknown number of classes and the definition of classes using binary states are among the targets of inference. We use a Bayesian approach to RCLMs in order to use informative prior assumptions on the number and definitions of latent classes to be consistent with scientific knowledge so that the posterior distribution tends to concentrate on smaller numbers of clusters and sparser binary patterns. The paper derives a posterior sampling algorithm based on Markov chain Monte Carlo with split-merge updates to efficiently explore the space of clustering allocations. Through simulations under the assumed model and realistic deviations from it, we demonstrate greater interpretability of results and superior finite-sample clustering performance for our method compared to common alternatives. The methods are illustrated with an analysis of protein data to detect clusters representing autoantibody classes among scleroderma patients.

Keywords: Autoimmune disease; Clustering; Dependent Binary Data; Latent Class Models; Markov Chain Monte Carlo; Mixture of Finite Mixture Models.

Notable Features

Special Case: Binary Matrix Factorization

This paper introduces a Bayesian framework that includes binary matrix factorization (BMF) as a special case (with unknown number of active latent dimensions and unknown number of distinct binary individual latent states). See the following illustration for an orthogonal decomposition:

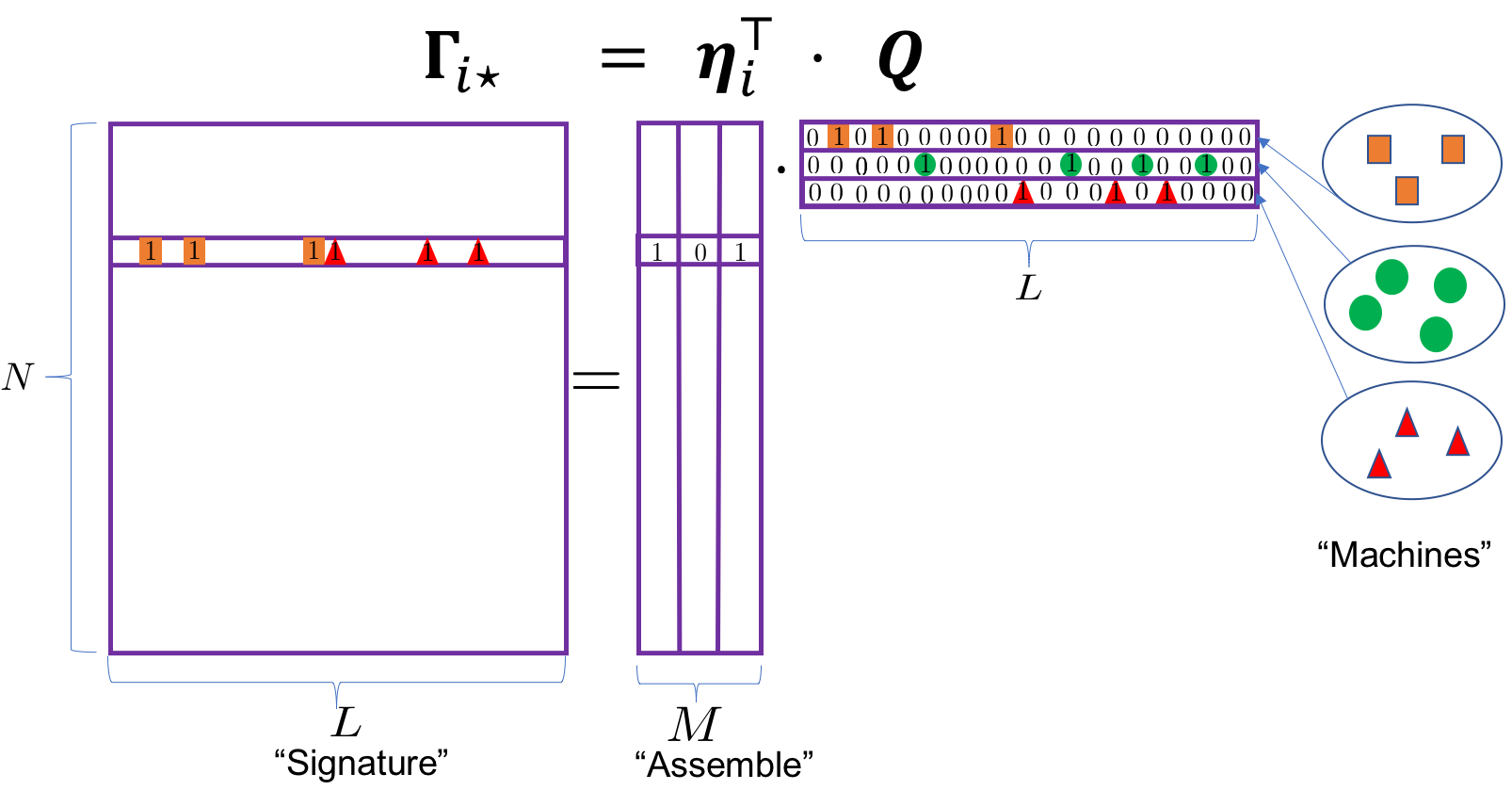Figure 1: Binary matrix factorization generates composite autoantibody signatures that are further subject to misclassification. The sigatures assemble three orthogonal machines with 3, 4 and 3 landmark proteins, respectively. The highlighted individual is expected to mount immune responses against antigens in Machines 1 and 3. See texts after model (6).

Superior Clustering Performance Compared to Hierarchical Clustering, All-feature Latent Class Analysis and Subset Clustering

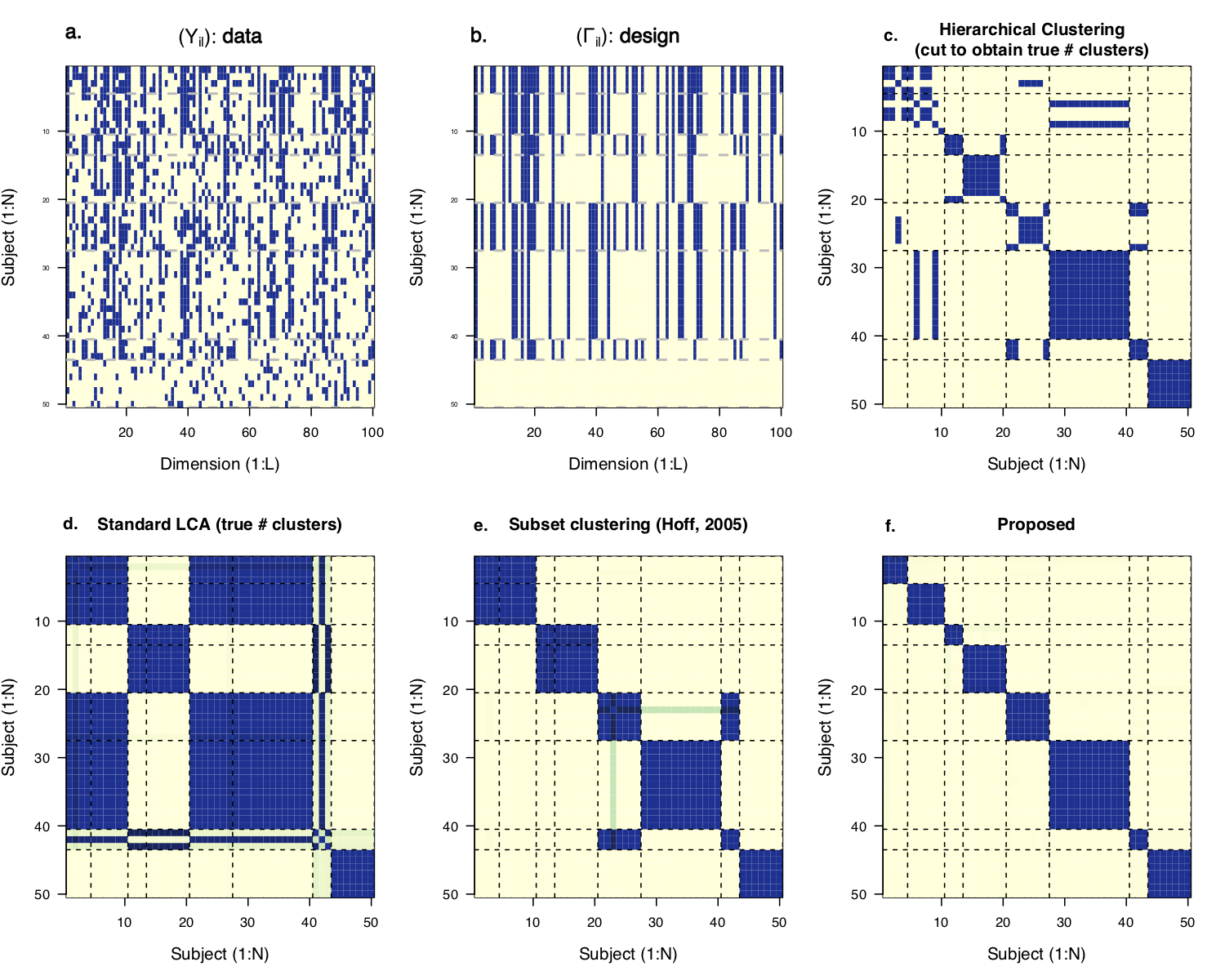Figure 2: In the 100-dimension multivariate binary data example, the eight classes differ with respect to subsets of measured features. Bayesian restricted latent class analysis accounts for measurement errors, selects the relevant feature subsets and filters the subsets by a low-dimensional model (like the one in the figure above) and therefore yields superior clustering results.