Abstract

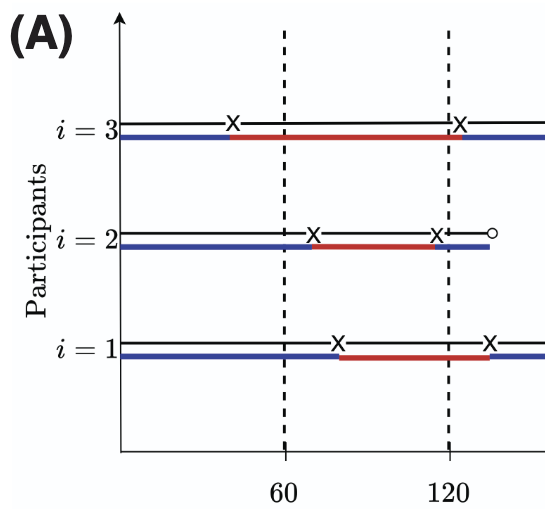
Alternating recurrent events, where subjects experience two potentially correlated event types over time, are common in healthcare, social, and behavioral studies. Often there is a primary event of interest that, when triggered, initiates a period of treatment and recovery measured via a secondary time-to-event. For example, cancer patients can experience repeated blood clotting emergencies that require hospitalization followed by discharge, people with alcohol use disorder can have periods of addiction and sobriety, or care partners can experience periods of depression and recovery. Potential censoring of the data requires special handling. Overlaying this are the missing at-risk periods for the primary event type when individuals have initiated the primary event but not reached the subsequent secondary event. In this paper, we develop a framework for regression analysis of censored alternating recurrent events that uses a random forest inverse probability weighting strategy to avoid bias in the analysis of the time to the primary event due to informative missingness from the alternate secondary state. The proposed regression model estimates $\tau$-restricted mean time to the primary event of interest while taking into account complexities of censored. Simulations show good performance of our method when the alternate times-to-event are either independent or correlated. We analyze a mobile health study data to evaluate the impact of self-care push notifications on the mental state of caregivers of traumatic brain injury patients.

Keywords Alternating recurrent events; Censored data; Inverse probability weighting; Longitudinal data; Pseudo-observations; Random forest.